Le point de départ de mon questionnement

Les élèves qui bénéficient de l’appui du dispositif ULIS collège que je coordonne ne connaissaient pas, sauf trois, le calcul littéral. Nous sommes en se moment dans une grande tendance collectif, avec la Course aux nombres de groupe, adaptée, alors j’ai eu envie d’y impliquer tout le monde, de la 6e à la 3e : deux questions de la Course concernent le calcul littéral et sont échouées. Comme les élèves progressent beraucoup plus vite que ce que j’avais prévu, je dois avancer vers les questions échouées massivement.

Mon but est d’arriver à ce que les élèves répondent à cette question, par exemple :

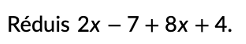
Mais comment ?

Le plan de bataille

Avec des élèves tels que ceux que j’accompagne, plusieurs difficultés spécifiques sont à prendre en compte :

• Les progrès doivent être rapides ;
• Les élèves doivent résister en cas d’erreur, ne pas décrocher ;
• L’accès à l’abstraction est difficile ;
• Les élèves ont une faible mémoire de travail ;
• Les élèves doivent visualiser leurs progrès ;
• Beaucoup de mes élèves sont de petits compteurs.

Ce weekend, j’ai réfléchi avec mon mari. J’ai décidé de passer par du matériel, pour compenser la mémoire de travail, garder une trace juste sous les yeux. Cela me permet aussi de soutenir les petits compteurs, qui peuvent s’y reprendre à autant de fois qu’ils le souhaitent.

Pour résister et ne pas abandonner en cas d’erreurs, y compris répétées, j’ai choisi d’utiliser l’ardoise, car on peut effacer ce qu’on a écrit sans traces, sans voir les multiples essais éventuellement infructueux.

Autre moteur de motivation : viser explicitement la réussite à la question de la Course aux nombres adaptée. Cela indique dès le départ qu’on se donne un objectif technique, et m’a permis d’éviter jusqu’ici la question de l’utilité. Bien sûr, nous allons aborder cette question, mais si je traite en même temps concept et technique, je pense perdre une partie des élèves, voire tous, justement en raison du problème d’accès à l’abstraction et de mémoire de travail faible.

Dernier levier de motivation : l’effet groupe. On apprend ensemble, on fait ensemble, les élèves inventent ensuite des exercices eux-mêmes, se vérifient, se corrigent et je régule tranquillement (en fait je bois du petit lait avec délectation, devant leurs réussites formidables).

Pour garantir des progrès rapides, j’ai décidé de monter progressivement le niveau. Partir de cas simples et bien consolider avant d’avancer. Mais en fait en une heure les élèves ont progressé de façon étonnante, et j’ai pu leur fixer des défis, complexifier en leur faisant systématiquement verbaliser ce qui devenait plus difficile. Ainsi, ils ont aussi identifié leurs progrès.

Autrement dit, les trois besoins fondamentaux sont assurés, en principe :

• le sentiment d’appartenance car tout le groupe travaille à la même chose, se soutient, s’encourage et coconstruit les énoncés une fois les premiers pas effectués,
• le sentiment d’autonomie car chacun a son matériel, mais peut aussi l’abandonner pour dessiner la situation puis « juste » effectuer les calculs,
• le sentiment de réussite, de compétence, parce qu’on va progresser !

Premiers objectifs

Pour ce début de semaine, j’ai visé de résoudre des calculs de ce type :

C’est un début seulement, nous sommes d’accord. Mais un bon gros début, déjà, pour tous ces élèves qui ignoraient le calcul littéral hier.

Le dispositif mis en place

Mon dispositif est tout simple :

Hier, nous avons travaillé avec du matériel découpé et complété ensemble à l’arrache. Des cartons x, des cartons 1, et zou, une expression, on représente avec les bouts de papier et on réduit en assemblant ce qui est de même nature.

Deux élèves ont demandé ce que c’était « x » (j’ai répondu : un nombre, mais on ne sait pas lequel, il est caché. Plus tard, nous allons résoudre des problèmes grâce à ces « x »). Deux ont tenté de réunir les papiers x et les papiers 1 en une seule catégorie, mais se sont ravisés : ce n’était pas la même chose qui était écrite.

Dès le départ, les élèves ont réussi, avec des erreurs ponctuelles et des questionnements initiaux.

Dès la première séance, j’ai proposé, pour ceux qui le souhaitaient, de lâcher le matériel et de représenter sur l’ardoise, en justifiant cette proposition par le fait que les étayages, c’est fait pour s’en passer. D’ailleurs le dessin aussi, ai-je annoncé, est une étape intermédiaire, mais bientôt les élèves auront tout dans la tête.

Aujourd’hui, j’ai anticipé et imprimé et découpé du matériel plus « professionnel » :

Même principe : les élèves ont des réductions à effectuer, ils utilisent le matériel (ou non, car très rapidement ils le lâchent) :

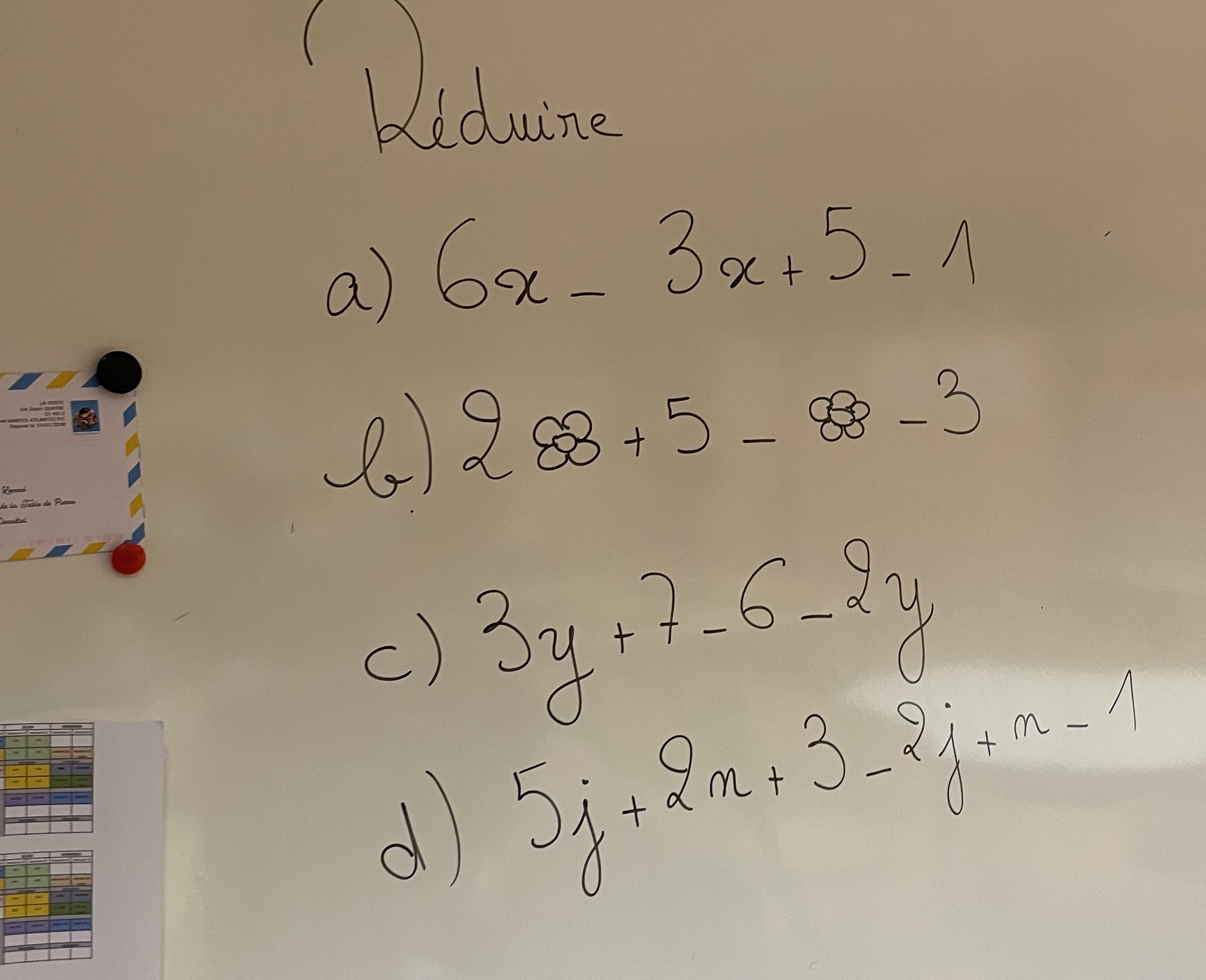
Premier bilan

Les élèves ont tous accédé aux niveaux que j’ai définis ci-dessus : tout le monde parvient à réduire des expressions avec plusieurs inconnues, même avec des soustractions. Mais je n’ai pas abordé de cas dans lesquels des coefficients seraient négatifs dans le résultat.

Ce que j’ai trouvé particulièrement intéressant, c’est que :

• Personne n’a été déstabilisé par les termes  » + x  » : souvent, les élèves ne tiennent pas compte du  » + x  » dans une expression (comme dans 3x + x), car le fait qu’ils ne voient pas de coefficient les amène à penser que ce coefficient est 0. Là,  » + x  » amène à ajouter un papier x, et voilà. C’est passé naturellement, et demeuré lorsque le matériel est abandonné ;
• Aucun élève n’a eu d’interrogation lorsque j’ai proposé deux inconnues au lieu d’une, comme des x et des t. Il y avait des papiers x, des papiers t, alors hop on obtient une somme de trois termes (avec les constantes) et c’est tout. Et ensuite, pour ceux qui ont laissé de côté le matériel, je peux mettre les symboles que je veux, tout passe bien. Demain je ramène des x au carré ;
• Lorsque j’ai introduit des soustractions, aucune hésitation non plus : les élèves ont enlevé des papiers qu’ils avaient positionnés au travers des additions.

Ce qui me paraît le meilleur des signes, c’est qu’après une heure (ou deux pour certains élèves) de travail, tout le monde a abandonné le matériel, mais est allé le rechercher lorsque la situation se complexifiait, pour ensuite le ré-abandonner. Cela signifie que les élèves ont pris ce matériel en main, mais savent que c’est un appui dont nous cherchons à nous passer. En plus ils ne me demandent rien : ils vont prendre des papiers, viennent les redéposer quand ils n’en ont plus besoin, et c’est tout.

Et puis ils étaient enthousiastes : comprendre, c’est tellement délicieux…

Ce matin, une élève est revenue tout fière :

Regarde, hier en rentrant du collège au foyer j’ai expliqué ça à tout le monde, et j’ai fait plein d’exercices et j’en ai fait faire plein aux autres !

Conclusion (provisoire)

Évidemment tout cela est bien joli, mais cela ne suffit pas à résoudre le calcul de la course aux nombres évoquée en début d’article : il va falloir que les élèves comprennent que 2x – 7 + 8x + 4 = 2x + 8x +4 – 7 et accèdent aussi au calcul de relatifs. Pour cela, il doivent déjà s’être affranchis de la manipulation et de la représentation, et avoir progressé conceptuellement, ce qui est le but du jeu.

Mais ça va le faire. Cela part super bien et ils ont déjà réussi très aisément bien au-delà de mes espérances. Ils ont travaillé une heure hier et ont su tout réactiver tout seuls aujourd’hui, en allant plus loin. Ils ont vu qu’ils apprenaient, qu’ils progressaient, ont travaillé ensemble, réussissent et en redemandent.

Pour moi, c’est une grande source de fierté et c’est extraordinairement motivant.