Après l’entrée en matière qui permet de s’exprimer et de se comprendre, avec Première partie : dire, lire et écrire les fractions, voici une assez courte deuxième étape de la séquence de découverte ou de remédiation des fractions : créer ses premières images mentales de fractions.

Les élèves ont parfois d’importantes difficultés à se créer des images mentales. Ce qui peut nous sembler aisé ne l’est pas forcément pour eux, entre autres pour cette raison : lorsque nous enseignons un concept, nous avons en tête des images mentales qui apparaissent, s’adaptent à la situation, correspondent à la nature dudit concept. Les élèves, pas toujours. C’est même un euphémisme : demandez à vos élèves de décrire comment ils se représentent telle ou telle notion, même géométrique. Pour ma part, j’ai été surprise : de nombreux élèves répondent par des propriétés plus ou moins bien formulées, en général signifiantes, mais par des paroles qui attestent de l’existence d’une image mentale, rarement.

Pour l’exercice de la pensée mathématique, c’est très embêtant : comme notre objectif est l’abstraction, il va bien falloir abandonner le matériel à un moment donné, et même la représentation écrite ou dessinée de façon figurative. Il va falloir entrer en soi et former des images (qui ne sont pas forcément ce qu’on entend par image couramment) qui nous donnent à voir avec le cerveau ce dont nous parlons, ce à quoi nous pensons, quel objet commun nous étudions.

L’enjeu est bien là : pouvoir échanger pour progresser autour d’un objet commun.

Pour la fraction, cela semble assez simple, et on peut même se demander pourquoi il faudrait abandonner la représentation figurative : on dessine une forme, on la sépare en parts équitables et on sélectionne un certain nombre de ces parts.

C’est simple à mettre en oeuvre et même à tester, en effet. C’est l’objet de cette fiche, appuyée sur le manuel Nouveaux outils pour les maths, édité chez Magnard.

Voici comment j’ai construit cette petite fiche :

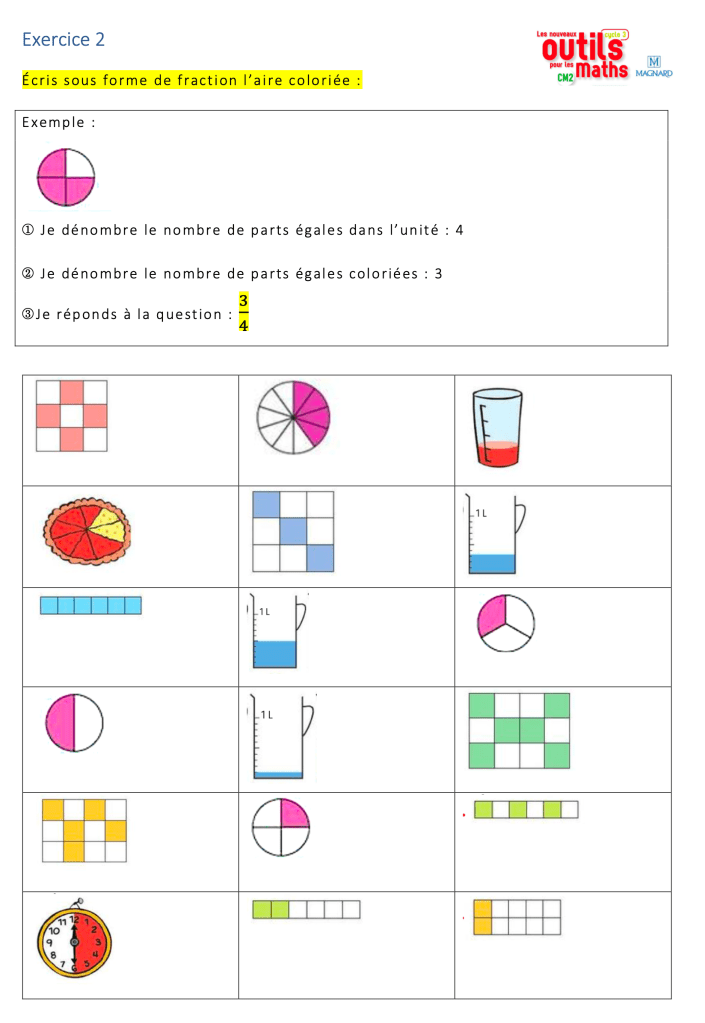
• La consigne est annoncée au début et surlignée en jaune, comme j’ai l’habitude de le faire, pour que les élèves qui sont déconcentrés à un moment donné ou qui ont une faible mémoire de travail puissent raccrocher ;
• Un exemple est proposé en encadré pour favoriser l’autonomie. L’élève ne doit pas en prendre connaissance seul, s’il s’agit d’une découverte : l’enseignant explique de quoi on parle, en insistant sur le fait que le partage se fait en parts égales. Il veille à reformuler et faire reformuler par les élèves autant que possible. Cela étant, même si c’est de la consolidation, il faudra réexpliciter tout ceci aussi ;
• La police, les espacements sont pensés pour une lecture plus aisée, et la consigne est composée du moins de mots possible ;
• Les propositions sont adaptées à une découverte de la fraction, avec des représentations de nombres tous inférieurs à l’unité, au tout ;
• Les formes présentées sont variées, évoquent deux ou trois dimensions, et les parts sélectionnées sont en effectifs différents et disposées différemment aussi ;
• Les images proposées peuvent faire appel à des grandeurs mesurées par des unités.

L’objectif est donc la multireprésentation, un peu à l’image des fleurs des nombres : on ne peut comprendre une nature de nombre qu’en multipreprésentant, puisque la représentation n’est pas le nombre.

Une autre fiche suit, pour réactiver, consolider voire approfondir. Cette fois j’ai utilisé des contenus de À portée de maths CM1 (Hachette) et Graine de maths CM2 (Nathan) :

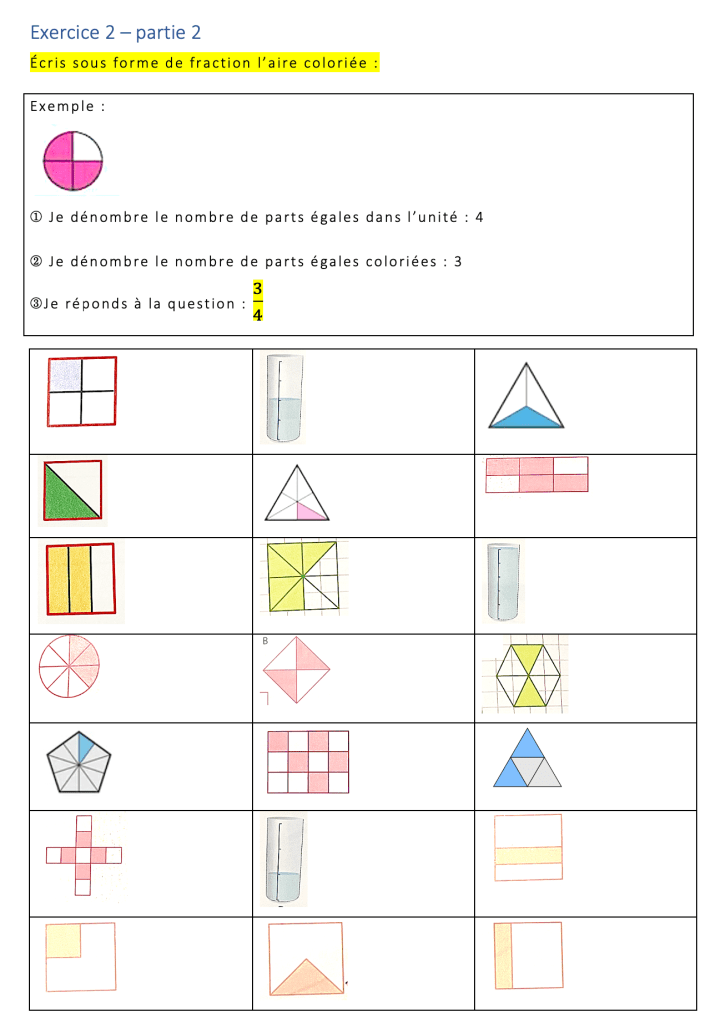
Des triangles, un pentagone, un hexagone et un dodécagone viennent apporter un peu de variété, et on termine sur des figures sur lesquelles le découpage n’est pas explicitement indiqué, et sur lesquelles il faut tracer des repères pour pouvoir répondre de façon assurée.

Cette double fiche arrive en étape 2 car, après l’indispensable prérequis de la verbalisation et de la compréhension orale, il faut s’engager dans la compréhension de ce qu’est la fraction. Ces dessins vont amener à l’idée de partage équitable, mais cela ne suffit pas du tout pour accéder à la compréhension de la fraction en tant que nombre. Le projet, c’est d’utiliser ces représentations comme passage, pour s’en affranchir plus tard, après avoir traversé la bande graduée puis l’axe gradué.

Des exercices tels que celui-ci, de l’académie de Poitiers, sont également à associer à cette étape :

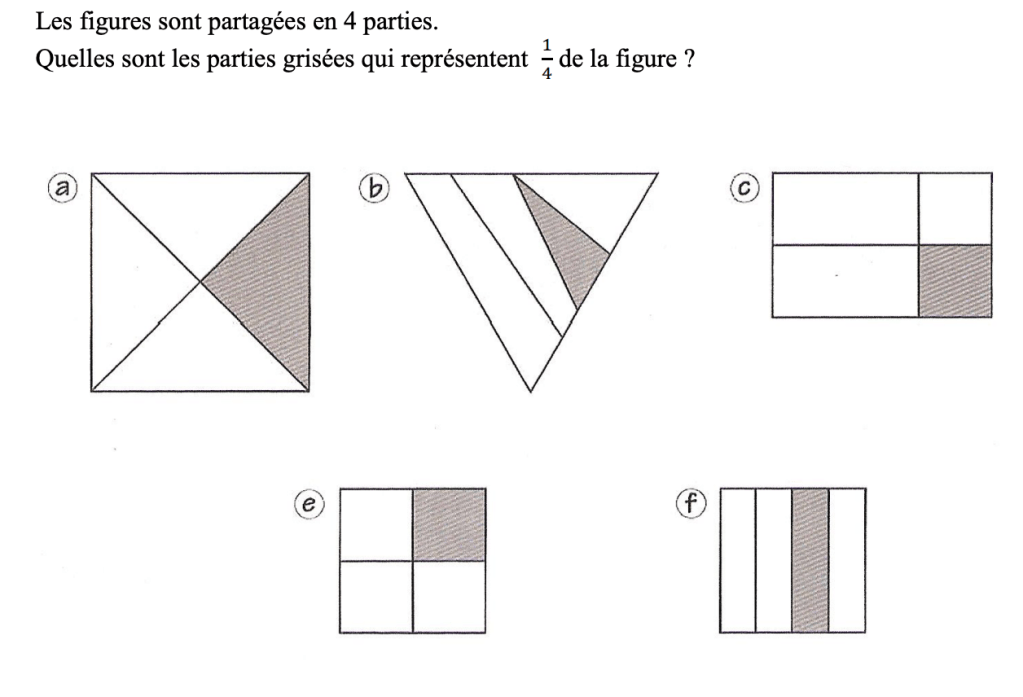
En effet, il s’agit de ne pas construire le réflexe « je compte les morceaux », mais de continuer à raisonner en permanence, de progresser dans le sens.